If 0.01 M Hcl Is Added to Pure Water, What Is the [oh-] in That Solution?

Chapter 14. Acid-Base Equilibria

14.2 pH and pOH

Learning Objectives

By the end of this department, you volition be able to:

• Explain the characterization of aqueous solutions as acidic, bones, or neutral
• Express hydronium and hydroxide ion concentrations on the pH and pOH scales
• Perform calculations relating pH and pOH

As discussed earlier, hydronium and hydroxide ions are nowadays both in pure water and in all aqueous solutions, and their concentrations are inversely proportional as determined by the ion product of water (K _w). The concentrations of these ions in a solution are often critical determinants of the solution's properties and the chemical behaviors of its other solutes, and specific vocabulary has been developed to describe these concentrations in relative terms. A solution is neutral if it contains equal concentrations of hydronium and hydroxide ions; acidic if it contains a greater concentration of hydronium ions than hydroxide ions; and bones if it contains a lesser concentration of hydronium ions than hydroxide ions.

A common means of expressing quantities, the values of which may bridge many orders of magnitude, is to use a logarithmic scale. One such scale that is very pop for chemical concentrations and equilibrium constants is based on the p-part, divers as shown where "X" is the quantity of involvement and "log" is the base-x logarithm:

[latex]\text{pX} = -\text{log\;Ten}[/latex]

The pH of a solution is therefore defined as shown here, where [H₃O⁺] is the molar concentration of hydronium ion in the solution:

[latex]\text{pH} = -\text{log[H}_3\text{O}^{+}][/latex]

Rearranging this equation to isolate the hydronium ion molarity yields the equivalent expression:

[latex][\text{H}_3\text{O}^{+}] = 10^{-\text{pH}}[/latex]

Likewise, the hydroxide ion molarity may be expressed as a p-function, or pOH:

[latex]\text{pOH} = -\text{log[OH}^{-}][/latex]

or

[latex][\text{OH}^{-}] = 10^{-\text{pOH}}[/latex]

Finally, the relation betwixt these ii ion concentration expressed every bit p-functions is hands derived from the G _w expression:

[latex]K_{\text{west}} = [\text{H}_3\text{O}^{+}][\text{OH}^{-}][/latex]

[latex]-\text{log}\;K_{\text{due west}} = -\text{log([H}_3\text{O}^{+}][\text{OH}^{-}]) = -\text{log[H}_3\text{O}^{+}]\;+\;-\text{log[OH}^{-}][/latex]

[latex]\text{p}K_{\text{due west}} = \text{pH}\;+\;\text{pOH}[/latex]

At 25 °C, the value of Yard _w is i.0 × x⁻¹⁴, and so:

[latex]fourteen.00 = \text{pH}\;+\;\text{pOH}[/latex]

As was shown in Example 1 in Affiliate xiv.1 Brønsted-Lowry Acids and Bases, the hydronium ion molarity in pure h2o (or whatever neutral solution) is i.0 × 10^−seven M at 25 °C. The pH and pOH of a neutral solution at this temperature are therefore:

[latex]\text{pH} = -\text{log[H}_3\text{O}^{+}] = -\text{log}(one.0\;\times\;10^{-7}) = 7.00[/latex]

[latex]\text{pOH} = -\text{log[OH}^{-}] = -\text{log}(one.0\;\times\;ten^{-seven}) = 7.00[/latex]

And so, at this temperature, acidic solutions are those with hydronium ion molarities greater than 1.0 × x^−vii M and hydroxide ion molarities less than 1.0 × ten⁻⁷ Chiliad (corresponding to pH values less than vii.00 and pOH values greater than 7.00). Basic solutions are those with hydronium ion molarities less than 1.0 × 10⁻⁷ One thousand and hydroxide ion molarities greater than i.0 × 10⁻⁷ M (corresponding to pH values greater than 7.00 and pOH values less than 7.00).

Since the autoionization constant G _w is temperature dependent, these correlations betwixt pH values and the acidic/neutral/basic adjectives will be dissimilar at temperatures other than 25 °C. For example, the "Check Your Learning" exercise accompanying Case 1 in Affiliate 14.ane Brønsted-Lowry Acids and Bases showed the hydronium molarity of pure water at eighty °C is four.9 × 10^−seven M, which corresponds to pH and pOH values of:

[latex]\text{pH} = -\text{log[H}_3\text{O}^{+}] = -\text{log}(four.9\;\times\;10^{-7}) = 6.31[/latex]

[latex]\text{pOH} = -\text{log[OH}^{-}] = -\text{log}(4.9\;\times\;x^{-7}) = six.31[/latex]

At this temperature, then, neutral solutions showroom pH = pOH = vi.31, acidic solutions exhibit pH less than half dozen.31 and pOH greater than 6.31, whereas bones solutions showroom pH greater than six.31 and pOH less than half-dozen.31. This distinction tin can exist important when studying certain processes that occur at nonstandard temperatures, such as enzyme reactions in warm-blooded organisms. Unless otherwise noted, references to pH values are presumed to be those at standard temperature (25 °C) (Table 1).

Classification	Relative Ion Concentrations	pH at 25 °C
acidic	[H3O+] > [OH−]	pH < 7
neutral	[H3O+] = [OH−]	pH = 7
basic	[H3O+] < [OH−]	pH > 7
Table 1. Summary of Relations for Acidic, Basic and Neutral Solutions

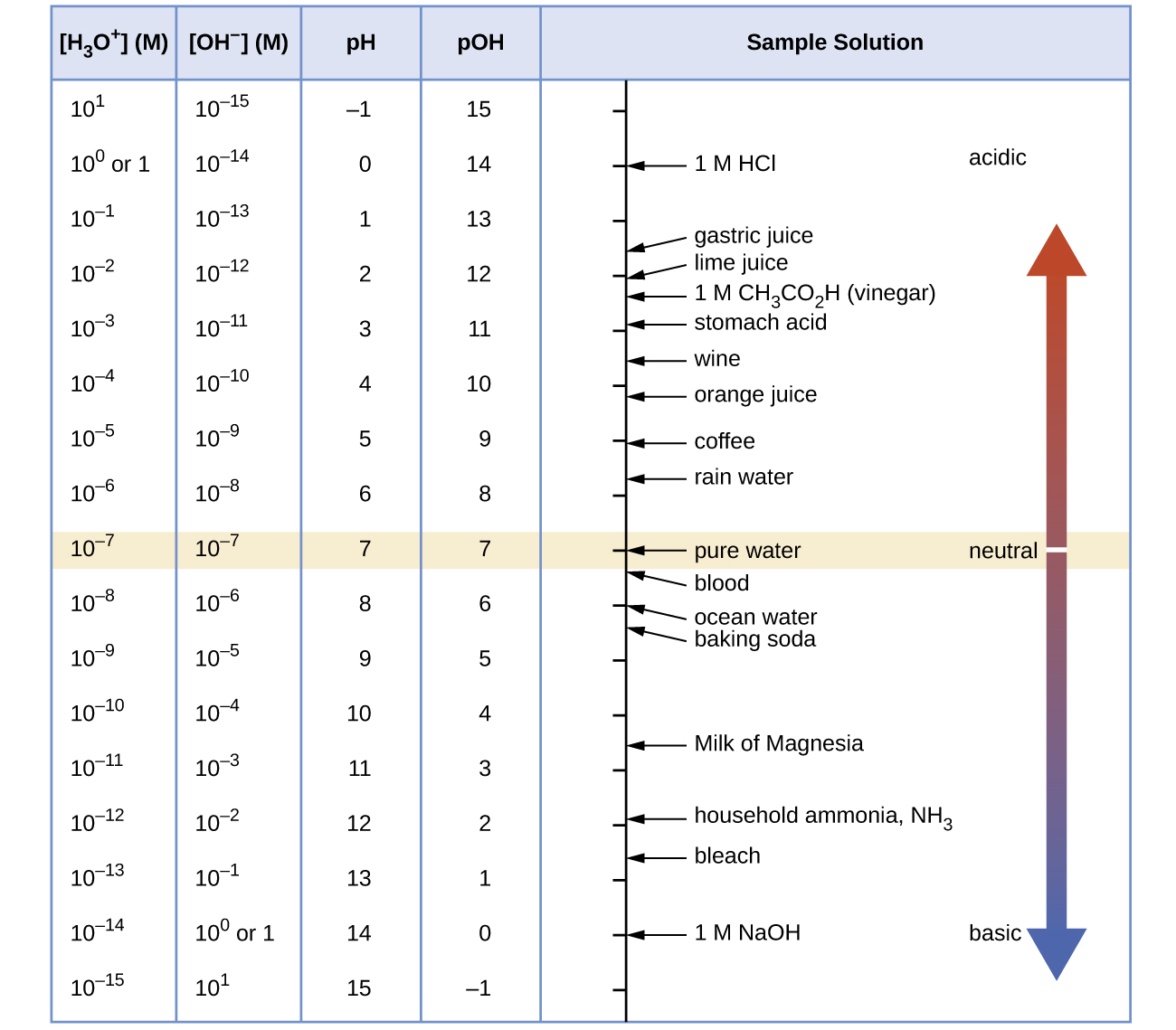
Figure one shows the relationships betwixt [H_iiiO⁺], [OH⁻], pH, and pOH, and gives values for these backdrop at standard temperatures for some common substances.

Figure i. The pH and pOH scales represent concentrations of [H₃O⁺] and OH⁻, respectively. The pH and pOH values of some common substances at standard temperature (25 °C) are shown in this chart.

Case 1

Calculation of pH from [H_threeO⁺]
What is the pH of tum acid, a solution of HCl with a hydronium ion concentration of i.ii × x⁻³ M?

Solution

[latex]\text{pH} = -\text{log[H}_3\text{O}^{+}][/latex]

[latex]= -\text{log}(i.2\;\times\;10^{-three})[/latex]

[latex]= -(-2.92) =2.92[/latex]

(The apply of logarithms is explained in Appendix B. Recall that, as nosotros have done hither, when taking the log of a value, keep as many decimal places in the event equally there are meaning figures in the value.)

Check Your Learning
Water exposed to air contains carbonic acrid, H_twoCO₃, due to the reaction between carbon dioxide and water:

[latex]\text{CO}_2(aq)\;+\;\text{H}_2\text{O}(l)\;{\leftrightharpoons}\;\text{H}_2\text{CO}_3(aq)[/latex]

Air-saturated water has a hydronium ion concentration caused past the dissolved CO₂ of two.0 × ten^−six M, about twenty-times larger than that of pure h2o. Calculate the pH of the solution at 25 °C.

Example ii

Calculation of Hydronium Ion Concentration from pH
Calculate the hydronium ion concentration of blood, the pH of which is 7.3 (slightly alkali metal).

Solution

[latex]\text{pH} = -\text{log[H}_3\text{O}^{+}] = vii.three[/latex]

[latex]\text{log[H}_3\text{O}^{+}] = -vii.three[/latex]

[latex][\text{H}_3\text{O}^{+}] = ten^{-7.iii}\;\text{or}\;[\text{H}_3\text{O}^{+}] = \text{antilog\;of\;}\;-7.3[/latex]

[latex][\text{H}_3\text{O}^{+}] = 5\;\times\;ten^{-8}\;Thou[/latex]

(On a reckoner have the antilog, or the "inverse" log, of −vii.3, or summate 10^−7.3.)

Cheque Your Learning
Summate the hydronium ion concentration of a solution with a pH of −one.07.

Environmental Scientific discipline

Normal rainwater has a pH between 5 and 6 due to the presence of dissolved CO_two which forms carbonic acid:

[latex]\text{H}_2\text{O}(l)\;+\;\text{CO}_2(g)\;{\longrightarrow}\;\text{H}_2\text{CO}_3(aq)[/latex]

[latex]\text{H}_2\text{CO}_3(aq)\;{\rightleftharpoons}\;\text{H}^{+}(aq)\;+\;\text{HCO}_3^{\;\;-}(aq)[/latex]

Acrid rain is rainwater that has a pH of less than 5, due to a variety of nonmetal oxides, including CO₂, And then₂, SO₃, NO, and NO_ii being dissolved in the water and reacting with it to form not just carbonic acrid, only sulfuric acrid and nitric acid. The germination and subsequent ionization of sulfuric acid are shown here:

[latex]\text{H}_2\text{O}(l)\;+\;\text{SO}_3(g)\;{\longrightarrow}\;\text{H}_2\text{SO}_4(aq)[/latex]

[latex]\text{H}_2\text{So}_4(aq)\;{\longrightarrow}\;\text{H}^{+}(aq)\;+\;\text{HSO}_4^{\;\;-}(aq)[/latex]

Carbon dioxide is naturally present in the atmosphere because we and nigh other organisms produce it as a waste of metabolism. Carbon dioxide is also formed when fires release carbon stored in vegetation or when we burn wood or fossil fuels. Sulfur trioxide in the atmosphere is naturally produced by volcanic activeness, only it besides stems from burning fossil fuels, which have traces of sulfur, and from the process of "roasting" ores of metallic sulfides in metal-refining processes. Oxides of nitrogen are formed in internal combustion engines where the high temperatures make information technology possible for the nitrogen and oxygen in air to chemically combine.

Acid pelting is a particular problem in industrial areas where the products of combustion and smelting are released into the air without beingness stripped of sulfur and nitrogen oxides. In N America and Europe until the 1980s, it was responsible for the destruction of forests and freshwater lakes, when the acidity of the rain actually killed trees, damaged soil, and made lakes uninhabitable for all but the most acid-tolerant species. Acid rain likewise corrodes statuary and edifice facades that are fabricated of marble and limestone (Figure 2). Regulations limiting the amount of sulfur and nitrogen oxides that can be released into the atmosphere past industry and automobiles have reduced the severity of acid damage to both natural and manmade environments in Due north America and Europe. It is now a growing problem in industrial areas of China and Republic of india.

For farther information on acid rain, visit this website hosted past the U.s.a. Environmental Protection Agency.

Figure 2. (a) Acid pelting makes trees more than susceptible to drought and insect infestation, and depletes nutrients in the soil. (b) Information technology also is corrodes statues that are carved from marble or limestone. (credit a: modification of piece of work by Chris Yard Morris; credit b: modification of work past "Eden, Janine and Jim"/Flickr)

Example 3

Calculation of pOH
What are the pOH and the pH of a 0.0125-M solution of potassium hydroxide, KOH?

Solution
Potassium hydroxide is a highly soluble ionic compound and completely dissociates when dissolved in dilute solution, yielding [OH⁻] = 0.0125 Thou:

[latex]\text{pOH} = -\text{log[OH}^{-}] = -\text{log}\;0.0125[/latex]

[latex]= -(-ane.903) = 1.903[/latex]

The pH tin can be plant from the pOH:

[latex]\text{pH}\;+\;\text{pOH} = 14.00[/latex]

[latex]\text{pH} = 14.00\;-\;\text{pOH} = 14.00\;-\;1.903 = 12.10[/latex]

Cheque Your Learning
The hydronium ion concentration of vinegar is approximately iv × x⁻³ 1000. What are the corresponding values of pOH and pH?

Answer:

pOH = 11.6, pH = ii.iv

The acidity of a solution is typically assessed experimentally past measurement of its pH. The pOH of a solution is not usually measured, as it is easily calculated from an experimentally adamant pH value. The pH of a solution tin be directly measured using a pH meter (Effigy three).

Figure 3. (a) A research-grade pH meter used in a laboratory can have a resolution of 0.001 pH units, an accurateness of ± 0.002 pH units, and may toll in excess of $1000. (b) A portable pH meter has lower resolution (0.01 pH units), lower accuracy (± 0.2 pH units), and a far lower price tag. (credit b: modification of work by Jacopo Werther)

The pH of a solution may likewise be visually estimated using colored indicators (Figure 4).

Figure 4. (a) A universal indicator assumes a dissimilar color in solutions of different pH values. Thus, it can be added to a solution to determine the pH of the solution. The eight vials each contain a universal indicator and 0.i-M solutions of progressively weaker acids: HCl (pH = l), CH₃CO₂H (pH = 3), and NH₄Cl (pH = v), deionized water, a neutral substance (pH = 7); and 0.1-M solutions of the progressively stronger bases: KCl (pH = 7), aniline, C₆H₅NH₂ (pH = nine), NH3 (pH = eleven), and NaOH (pH = xiii). (b) pH newspaper contains a mixture of indicators that give dissimilar colors in solutions of differing pH values. (credit: modification of work by Sahar Atwa)

Central Concepts and Summary

The concentration of hydronium ion in a solution of an acid in water is greater than 1.0 × 10⁻⁷ Thou at 25 °C. The concentration of hydroxide ion in a solution of a base of operations in water is greater than one.0 × 10^−seven M at 25 °C. The concentration of [latex]\text{H}_3\text{O}^{+}[/latex] in a solution tin exist expressed as the pH of the solution; [latex]\text{pH} = -\text{log[H}_3\text{O}^{+}][/latex]. The concentration of OH⁻ can be expressed as the pOH of the solution: pOH = −log[OH⁻]. In pure water, pH = 7.00 and pOH = 7.00

Key Equations

• [latex]\text{pH} = -\text{log[H}_3\text{O}^{+}][/latex]
• pOH = −log[OH⁻]
• [H₃O⁺] = 10^−pH
• [OH⁻] = x^−pOH
• pH + pOH = pK _w = 14.00 at 25 °C

Chemical science Stop of Chapter Exercises

1. Explain why a sample of pure water at 40 °C is neutral fifty-fifty though [H₃O⁺] = 1.7 × x^−vii One thousand. Yard _w is 2.ix × x⁻¹⁴ at twoscore °C.
2. The ionization constant for h2o (Thou _west) is 2.nine × 10⁻¹⁴ at 40 °C. Summate [H₃O⁺], [OH⁻], pH, and pOH for pure water at 40 °C.
3. The ionization constant for water (K _w) is ix.311 × 10^−xiv at 60 °C. Calculate [H_iiiO⁺], [OH⁻], pH, and pOH for pure h2o at 60 °C.
4. Calculate the pH and the pOH of each of the following solutions at 25 °C for which the substances ionize completely:

   (a) 0.200 M HCl

   (b) 0.0143 M NaOH

   (c) 3.0 Thou HNO₃

   (d) 0.0031 M Ca(OH)_ii

5. Calculate the pH and the pOH of each of the following solutions at 25 °C for which the substances ionize completely:

   (a) 0.000259 M HClO₄

   (b) 0.21 K NaOH

   (c) 0.000071 One thousand Ba(OH)₂

   (d) 2.5 M KOH

6. What are the pH and pOH of a solution of ii.0 M HCl, which ionizes completely?
7. What are the hydronium and hydroxide ion concentrations in a solution whose pH is 6.52?
8. Calculate the hydrogen ion concentration and the hydroxide ion concentration in wine from its pH. See Figure one for useful information.
9. Calculate the hydronium ion concentration and the hydroxide ion concentration in lime juice from its pH. See Figure 1 for useful information.
10. The hydronium ion concentration in a sample of rainwater is constitute to exist ane.vii × 10^{−half-dozen} One thousand at 25 °C. What is the concentration of hydroxide ions in the rainwater?
11. The hydroxide ion concentration in household ammonia is 3.2 × 10⁻ⁱⁱⁱ One thousand at 25 °C. What is the concentration of hydronium ions in the solution?

Glossary

acidic

describes a solution in which [H₃O⁺] > [OH⁻]

bones

describes a solution in which [H₃O⁺] < [OH⁻]

neutral

describes a solution in which [H₃O⁺] = [OH⁻]

pH

logarithmic measure of the concentration of hydronium ions in a solution

pOH

logarithmic measure of the concentration of hydroxide ions in a solution

Solutions

Answers to Chemical science End of Affiliate Exercises

1. In a neutral solution [H₃O⁺] = [OH⁻]. At xl °C,
[H_iiiO⁺] = [OH⁻] = (2.910⁻¹⁴)^i/two = 1.7 × 10^−seven.

3. x = 3.051 × 10^−seven Grand = [H₃O⁺] = [OH⁻]
pH = −log3.051 × 10^−vii = −(−6.5156) = 6.5156
pOH = pH = 6.5156

5. (a) pH = 3.587; pOH = 10.413; (b) pH = 0.68; pOH = thirteen.32; (c) pOH = iii.85; pH = 10.15; (d) pH = −0.xl; pOH = 14.4

seven. [H₃O⁺] = three.0 × 10⁻⁷ G; [OH⁻] = 3.iii × 10⁻⁸ Thousand

9. [H₃O⁺] = i × 10⁻² Grand; [OH⁻] = 1 × 10⁻¹² M

xi. [OH⁻] = 3.1 × 10⁻¹² M

powellhishonce.blogspot.com

Source: https://opentextbc.ca/chemistry/chapter/14-2-ph-and-poh/

Share this post